Sala María Andresa Casamayor

Sólidos de anchura constante.

En el plano (en dos dimensiones), es bastante sencillo construir figuras de anchura constante. Para ello sólo se necesita un polígono regular (triángulo equilátero, cuadrado, pentágono, etc…) y un compás.

Las formas de anchura constante se utilizan, y hay bastantes ejemplos en países anglosajones, en la fabricación de monedas. Aunque esas monedas dan la sensación de que tienen esquinas, como su anchura es constante, ¡estamos seguros que no se atascarán en la máquina de refrescos!. También se han utilizado estas curiosas figuras como fuente de inspiración en pintura y arquitectura.

Cónicas.

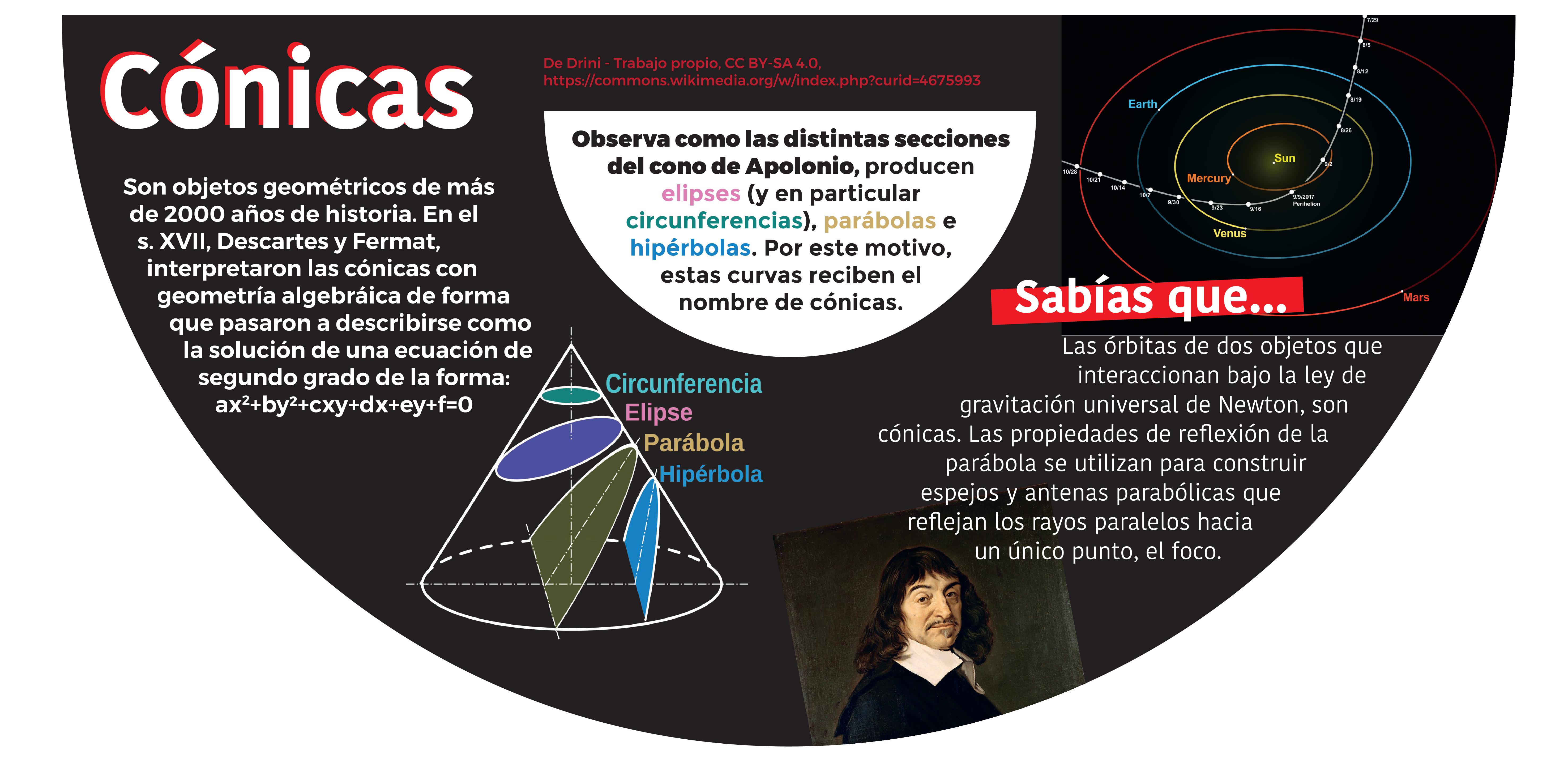
Circunferencias, elipses, parábolas e hipérbolas son curvas planas conocidas desde hace más de 2000 años. El matemático griego Apolonio de Pérgamo observó que todas ellas se producen cuando haces secciones en un cono. Desde entonces estas curvas reciben el nombre de cónicas.

Las cónicas comenzaron a ser estudiadas como un objeto geométrico, pero no tardaron en aparecer en los lugares más inesperados tanto en la naturaleza como en tecnología. Por ejemplo, las órbitas de dos objetos que interaccionan bajo la ley de gravitación universal de Newton, forman cónicas.

Desde el descubrimiento de Descartes, el álgebra parece haber superado a la geometría y estos objetos se suelen presentar a través de sus ecuaciones.

Cubo Soma.

El reto consiste en ordenar 7 piezas para formar un cubo de dimensiones 3×3×3. Si lo consigues, habrás obtenido una de las 240 soluciones distintas posibles. Puedes intentar otra solución que tenga distinta configuración. También proponemos la construcción de alguna otra estructura como las de las imágenes en el cartel. Ejercitar la visión espacial es el principal objetivo del reto.

En dos dimensiones, en lugar de tres, seguramente sea el Tangram, originario de China, el puzzle más conocido. Sus siete piezas están basadas en el ángulo de 45 grados.

El tangram de 8 piezas está basado en el ángulo de 60 grados e inventado/descubierto por el español Jaume Llibre en 1975.

¡¡Con pocas piezas se pueden generar multitud de figuras!!.

Estadística y Probabilidad.

Estas dos cajas están llenas de bolas verdes y rojas. Agita las cajas y observa la muestra en el lateral (tapado en negro) de bolas que puedes ver. La pregunta es ¿qué caja crees que tiene más bolas rojas?. Parece que con solamente un experimento es imposible saber la respuesta.

La Inferencia estadística tiene como uno de sus objetivos extraer información de una población grande a partir de muestras pequeñas escogidas de esa población. Repitiendo el experimento varias veces (es decir tomando varias muestras) se puede responder a la pregunta planteada. Aunque no es un sistema perfecto, hay un margen de error.

Las herramientas estadísticas y probabilísticas se utilizan en multitud de disciplinas que van desde la Sociología hasta la Biología. Incluso en muchos deportes se usa estadística para analizar rivales, saber qué aspectos mejorar o realizar fichajes.

Los puentes de Koenigsberg.

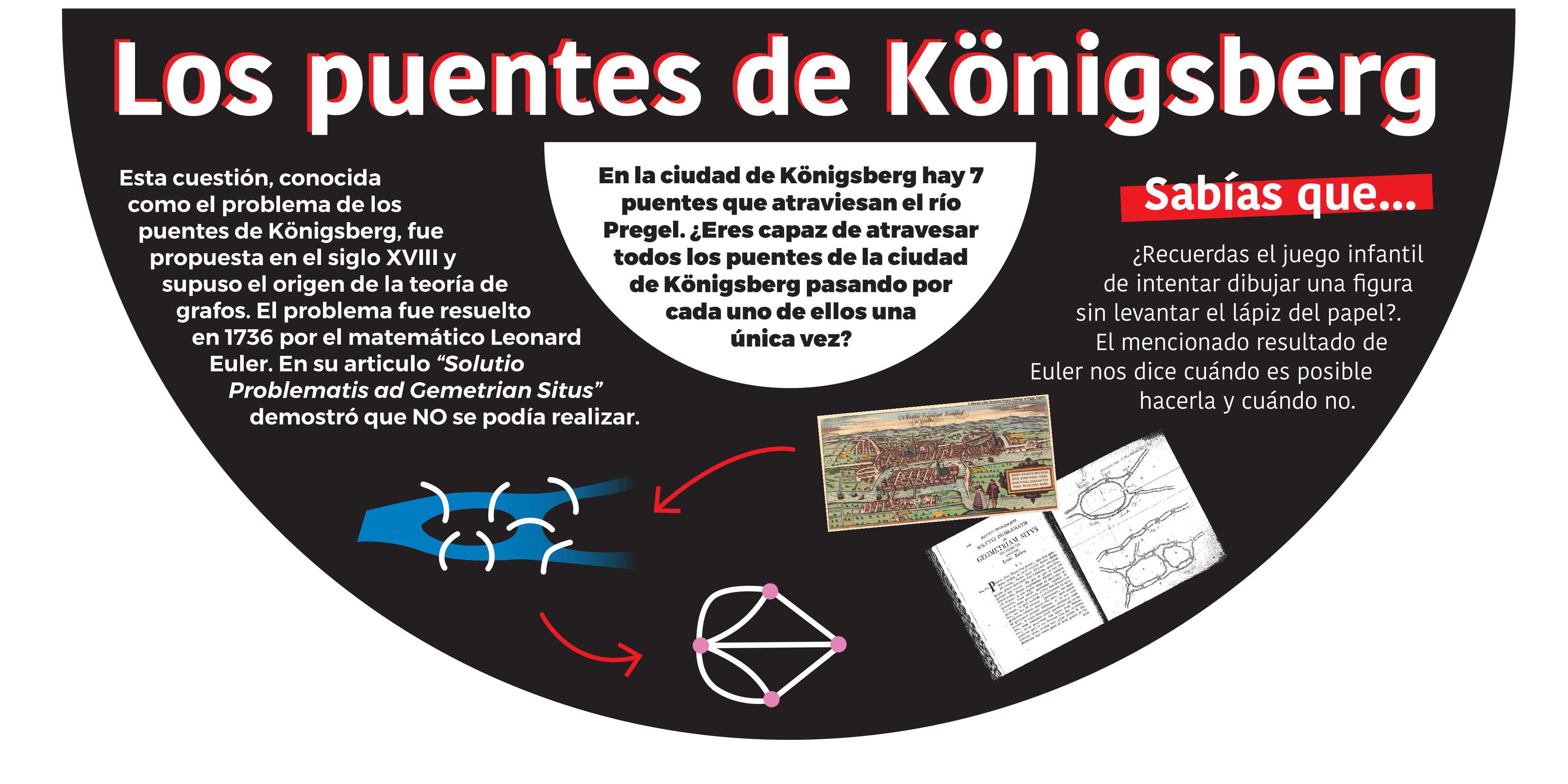
En la ciudad de Königsberg hay 7 puentes sobre el rio Pregel. Sus habitantes hacían el juego de pasear intentando atravesar todos los puentes pero pasando por cada uno de ellos una sola vez. Es decir, no se puede pasar dos veces por un mismo puente.

¿Eres capaz de hacerlo sobre la maqueta?. Usa tu dedo para ayudarte a seguir mejor tu paseo.

¿No te ha salido? Cambia un puente de lugar e inténtalo de nuevo. O si no, prueba apartando un puente.

A veces el problema tiene solución y a veces no, ¿verdad?. ¿Te atreverías dar una explicación de esto? Si has dado con la razón de cuando si y cuando no se puede realizar el juego, enhorabuena, estás al nivel del matemático Leonard Euler que inició en 1736 con este teorema la hoy llamada Teoría de Grafos.

Y para terminar, ¿Recuerdas el juego infantil de intentar dibujar una figura sin levantar el lápiz del papel y sin pasar dos veces por el mismo lugar?. Dependiendo del dibujo, a veces si puede dibujar y a veces no, ¿verdad?…Pues resulta que es el mismo juego que el de los puentes.

Mate-Magia.

Te proponemos un juego de Mate-magia para hacer a tu acompañante o si quieres ¡a tí mismo. ¡Necesitarás del monitor de sala para que te enseñe a ser un matemago!

Te avanzamos una pista para descubrir el truco. El juego está basado en las propiedades de par-impar.

Hay una buena colección de juegos de magia, por ejemplo con cartas, dados, palillos, billetes, monedas... que utilizan ingeniosos trucos basados en matemáticas. Algunos de éllos son simples propiedades aritméticas de números o geométricas de figuras que, con la habilidad de un buen mago, nos consiguen sorprender. Conocer el truco es… aprender matemáticas.

Martin Gardner es la figura más influyente y reconocida de la Mate-magia. Sus textos han influenciado a generaciones enteras de toda clase de aficionados a las matemáticas.

El cubo de Rubik.

Originalmente fue un diseño geométrico realizado por el escultor húngaro Ernö Rubik en 1974. Hoy en día es el juguete más vendido de la historia.  

El reto es conseguir que todas las caras de cubo sean de un solo color.

El canal Mathologer te enseña la forma de resolverlo eligiendo TU mismo tu movimiento básico favorito, el que tú prefieras.

El cubo clásico 3x3x3 tiene unos 43 quintillones de combinaciones. A pesar de ello, desde 2010 sabemos que siempre se puede resolver en sólo ¡20 movimientos !.

El record de resolverlo en menos tiempo está desde 2018 en manos de Yusheng Du. Lo resolvió en ¡¡ 3,47 segundos !! …. Es menos de lo que has tardado en leer esta frase hasta el final.

La variante más sencilla es el cubo 2x2x2 que tiene 3.674.160 combinaciones. Lo cual es bastante manejable. Si jugaras con un cubo 2x2 moviéndolo al azar, durante unas ocho horas al día, lo resolverías por pura casualidad unas dos o tres veces al año.

Superficies.

Una superficie es un objeto matemático de dos dimensiones que localmente se parece a un plano. No hay esquinas, no hay ángulos. Nuestra experiencia en el planeta Tierra, nos ayuda a entender qué queremos decir. Parece plana de cerca, pero globalmente la esfera la superficie que se adecúa mejor a nuestro planeta.

Globalmente, las superficies presentas muy variadas formas y aplicaciones:

Por ejemplo, las chimeneas de las centrales nucleares tienen la forma de hiperboloides de una hoja, obtenidos al girar una hipérbola sobre un eje de simetría.

Las antenas parabólicas son paraboloides que se obtienen al girar una parábola sobre su eje de simetría.

Los paraboloides hiperbólicos dan forma a tejados o cubiertas en arquitectura. Estos, además, tienen la sorprendente propiedad de que, aunque nos parecen curvadas a la vista, se pueden construir mediante vigas rectas.

En la mesa verás los modelos que corresponden a estos ejemplos.

Las torres de Hanoi.

Tienes que cambiar todos los discos hasta otro poste con la siguiente regla: Solo se puede mover UN disco cada vez y NUNCA se puede poner un disco más grande sobre uno más pequeño.

Para calentar, comienza el juego con solo tres discos. ¿Te ha salido?

Intenta ahora con cuatro discos. Te doy una pista, que te sonará simple pero es la clave de todo: Pasa primero tres discos tal y como lo has aprendido antes. Verás que vas a tener que pasar esos tres discos dos veces.

¿Lo intentas ahora con cinco?. Recuerda que la pista es: Pasa primero cuatro como lo has hecho antes.

Aunque a una persona le pueda costar un poco, hacer un programa de ordenador que resuelva este problema es especialmente sencillo. Torres de Hanoi es uno de los primeros ejemplos de bucle .