Sala Exterior

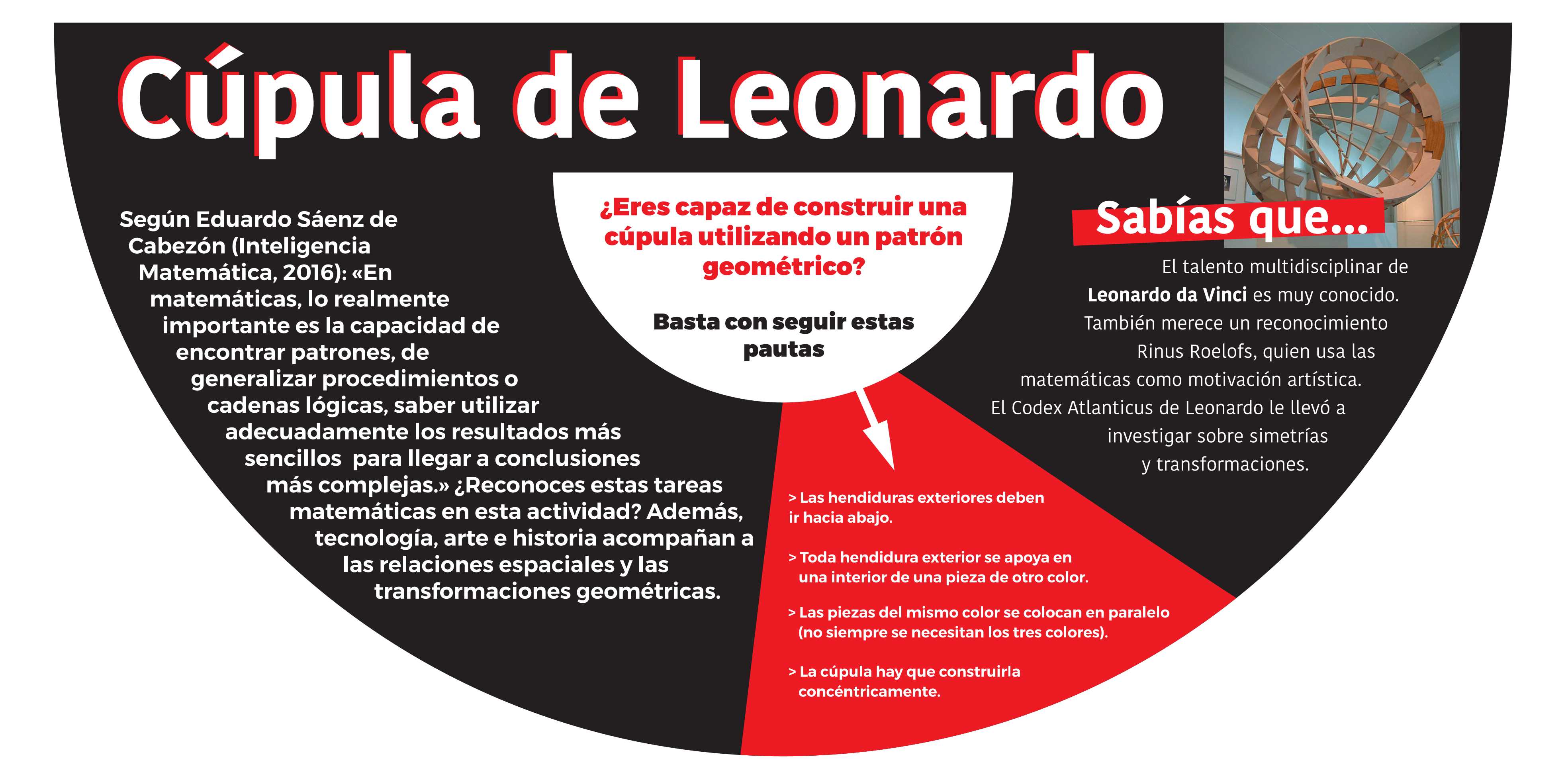
Cúpula de Leonardo.

Esta forma de construcción fue ideada por Leonardo da Vinci. Utiliza piezas con 4 muescas que se superponen entre sí. No es necesario ningún otro elemento de unión, el peso de las piezas es suficiente para mantener su estabilidad.

Para ayudarte a dar con el patrón de construcción hemos puesto piezas de colores que te facilitará su seguimiento. Las instrucciones disponibles en la mesa te ayudarán.

Las simetrías son la clave en cada uno de los modelos que proponemos.

En el exterior encontrarás una Cúpula de Leonardo de mayor tamaño, incluso ¡podrás meterte dentro!. Esta actividad en pequeño te vendrá muy bien para preparar la grande.

Espejos parabólicos.

Te proponemos dos experimentos:

1. Ponte las gafas de sol. Coloca un papel oscuro en el foco de la parábola y apunta el espejo parabólico hacia el sol. Sus rayos se concentran en el foco y...¿consigues que se caliente hasta que aparezca humo?.

2. Toma el micrófono parabólico y ponte los cascos. Pide a tus compañeros que se alejen y hablen susurrando. Si apuntas el micrófono hacia éllos... ¿puedes oir lo que dicen?

La propiedad seguramente más conocida de la parábola es que todo rayo paralelo a su eje se refleja hacia el foco… ¡y viceversa!, todos los rayos que se emiten desde el foco se reflejan como rayos paralelos.

Al girar una parábola plana alrededor de su eje, se genera una superficie, un paraboloide, que es el objeto que tienes a la vista.

La particular manera de reflejar sobre esta superficie hace que se utilice en çantenas parabólicas, faros de coches, altos hornos solares, cocinas solares etc…

En honor a sus descubridores, la antorcha olímpica de cada Olimpiada es encendida en Grecia con la luz del sol reflejada sobre un espejo parabólico.

Puente de Leonardo.

Leonardo da Vinci dejó varios dibujos de diseños de puentes en sus manuscritos. El recogido en el códice Atlántico se construye sin ningún tipo de ataduras ni clavos. El entrelazado de las vigas que lo forman y la acción de la gravedad, son suficientes para levantarlo y que además pueda soportar grandes pesos.

Este tipo de puentes representa una solución óptima para salvar pequeños obstáculos de una manera rápida. La dificultad estriba en el proceso de montaje, que el propio Leonardo dejó esquematizado en sus códices.

En el exterior encontrarás las piezas para confeccionar un puente de buen tamaño que puede aguantar tu propio peso. ¿Te animas a cruzarlo?

Puedes ver en este enlace cómo se construye.

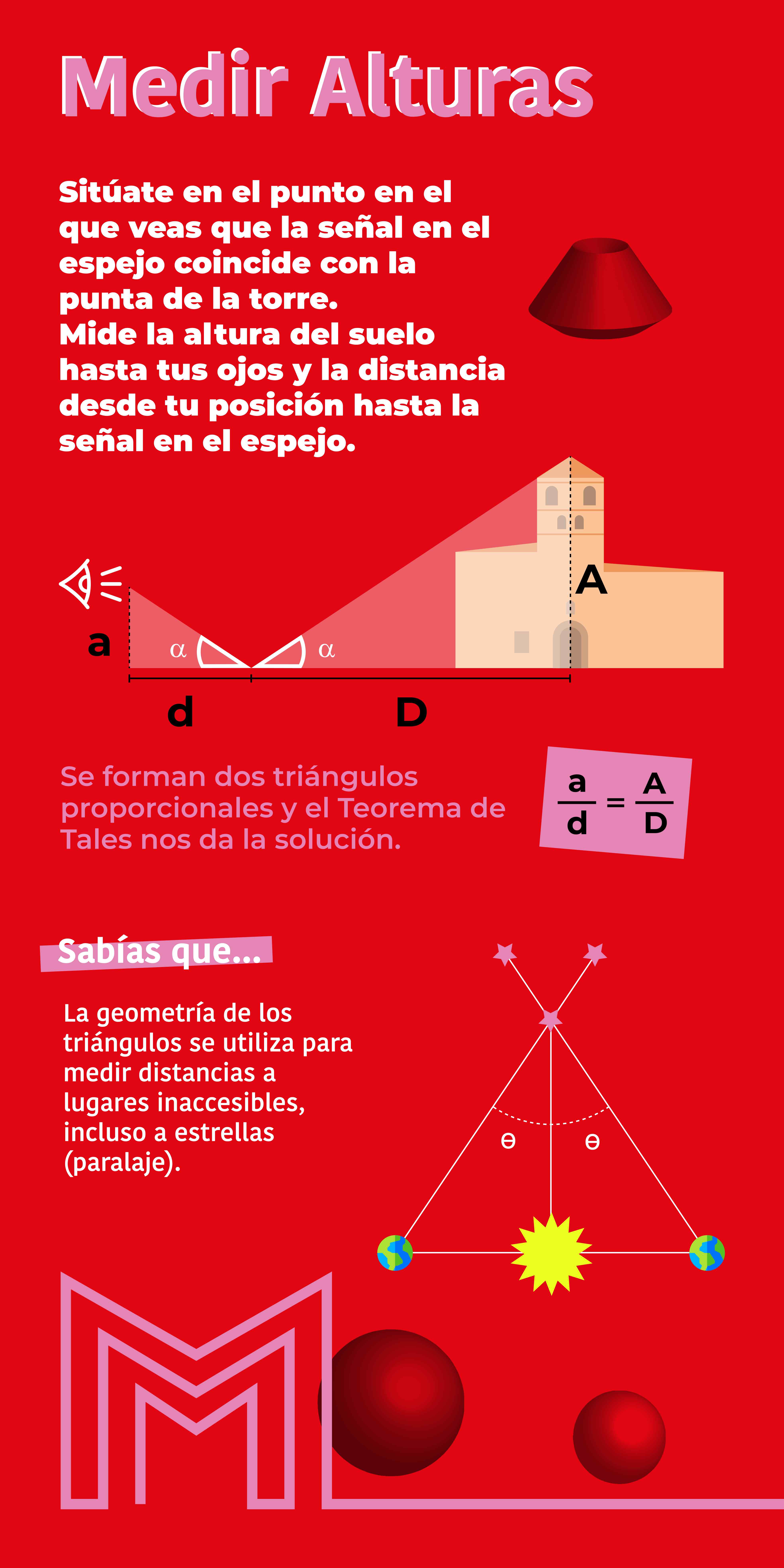
Medir alturas.

Sitúate en el punto en el que veas que la señal en el espejo coincide con la punta de la altura que queremos medir. Necesitas medir la altura del suelo hasta tus ojos y la distancia desde tu posición hasta la señal en el espejo.

En el experimento que proponemos verás que se forman dos triángulos semejantes y que el Teorema de Tales nos da la solución. Puedes repetir el experimento con otra persona a ver si sale la misma solución. Los errores de medición disminuyen situando el espejo más alejado de la altura a medir.

Medir distancias a puntos inaccesibles es uno de los más tempranos usos de la semejanza de triángulos descubiertos por Tales. Esta misma geometría se utiliza para medir distancias a la luna, al sol, a otros planetas e incluso a estrellas.

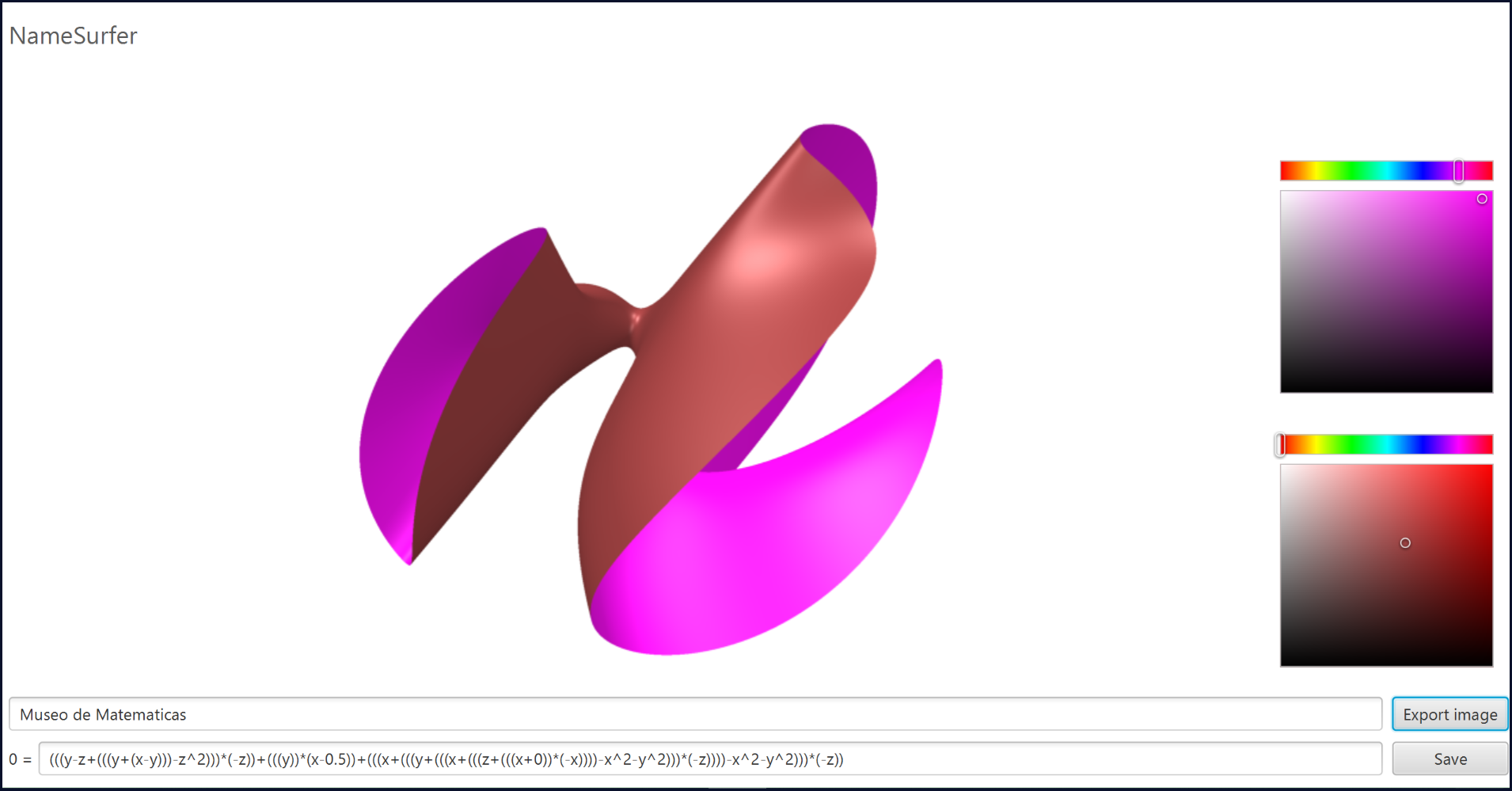
Superficies algebraicas.

NameSurfer es un programa de dibujo de superficies.

Su historia viene de lejos: En el siglo XVII se produjo la unión dos mundos: A un lado se encontraban las curvas y las superficies (parábolas, circunferencias, esferas etc…), es decir la geometría. Y por otro, las operaciones, los números, las ecuaciones… o sea el álgebra.

Quizá recuerdes haber estudiado las ecuaciones de las parábolas o de las rectas en el plano.

Pues bien, en dicho siglo el matemático R. Descartes descubrió que es posible describir los objetos geométricos a través de ecuaciones. Desde ese momento, números y curvas, ecuaciones y superficies quedaron unidas para siempre.

NameSurfer está preparado para que escribas por ejemplo tu nombre o lo que quieras. El programa transformará las letras escritas en una ecuación y es ésta la que aparecerá representada como superficie. Es el descubrimiento de Descartes de hace 400 años visto desde hoy.

Doble dominó.

Pon los ladrillos en fila, uno a continuación de otro sin dejar espacio. Levántalos sin desplazarlos, uno por uno hasta formar un “dominó”.

Empuja el primero y… ¡observa lo que ocurre!.

Para que el doble dominó funcione se necesita una relación adecuada entre el grosor y la longitud de los ladrillos Esta relación se resume en el cartel y está representada por dos triángulos proporcionales o semejantes.

Tales de Mileto en el siglo VI A.C. descubrió la importancia y las aplicaciones de la semejanza de triángulos.

Mosaicos.

Morenaments es un programa de dibujo de mosaicos.

Si has visto imágenes de los mosaicos de la Alhambra de Granada, o te has fijado en las paredes de las iglesias mudéjares en Aragón, quizá te hayas preguntado cómo conseguían esas decoraciones.

A partir de un trazo, el programa te mostrará todas las posibilidades de embaldosar usando tu trazo, para lo que usará los 17 grupos de simetrías posibles que consisten en combinaciones de giros, reflexiones y traslaciones.

Los artesanos árabes conocían bien los secretos de estas simetrías y eran capaces de hacer sus complejas decoraciones a partir de una única baldosa sin más que… ¡repetirla!.

La base son baldosas triangulares, cuadradas o hexagonales pues no hay ningún otro polígono regular que pueda embaldosar un plano.

Muchos siglos más tarde, cuando los geólogos estudiaban la formación de los cristales, descubrieron que la naturaleza se sirve de exactamente esos mismos grupos de simetrías, que desde entonces se llaman cristalográficos.