Sala María Teresa Lozano

Cicloide.

Deja caer las dos canicas a la vez desde el extremo, pero antes intenta adivinar: ¿Cuál llegará antes al final?. ¿La del camino recto? ¿La del camino curvo? ¿Llegarán a la vez?.

A pesar de que el camino más corto entre dos puntos es la línea recta, el camino más rápido de todos los posibles viene dado por la curva que ves, llamada cicloide.

Es por esto que las pistas de monopatín se construyen con forma de cicloide.

La cicloide tiene otra interesante propiedad. Toma una canica con cada mano, ponlas en cualquier posición sobre la cicloide y suéltalas a la vez. Da igual donde coloques las manos y desde donde las sueltes. Siempre llegarán abajo las dos a la vez. Repíte el experimento para comprobarlo.

Cuatro colores.

A mediados del siglo XIX, el abogado Francis Guthrie propuso el problema de colorear mapas con el menor número de colores posible. Se impone, claro, que dos países con frontera común NO puedan tener el mismo color.

En esta actividad proponemos colorear una esfera, con un poco de imaginación puedes pensar que es la Tierra.

Durante más de un siglo se pensó que cuatro colores bastaban para colorear cualquier mapa. Pero la demostración de esta intuición se resistía. Hay desde luego, muchos mapas más fáciles que hasta los puedes colorear con tan solo tres colores.

No fue hasta 1976 cuando se pudo demostrar por primera vez el teorema de los cuatro colores. La demostración pasaba por reducir las posibilidades a un número de casos inevitables. Pero ese número era muy alto, de varios miles, y se tuvo que utilizar un ordenador para verificarlos todos.

Comenzó entonces la discusión en la comunidad matemática de si era aceptable una demostración no realizada completamente con la mente y el razonamiento lógico. Durante otros 30 años se buscaron nuevas demostraciones que no necesitaran el uso de ordenador. Lo que finalmente se consiguió a inicios del siglo XXI.

Curiosamente, para colorear mapas que estuvieran sobre una rosquilla se necesitan en general siete colores.

Juegos de Nim.

En este juego, dos jugadores juegan por turnos. En cada turno, cada jugador debe quitar 1, 2 ó 3 fichas. Gana el jugador que se lleva las últimas fichas.

Los Juegos de Nim, son juegos por turnos en los que alguno de los dos jugadores tiene una estrategia ganadora. Eso quiere decir, que un jugador siempre gana si conoce esa estrategia, y no importa como juegue el otro jugador.

Te damos una pista para ganar siempre: En el juego con 13 fichas, el jugador que empieza tiene estrategia ganadora. La estrategia consiste en dejar siempre al otro jugador un número de fichas que sea múltiplo de 4. Primero, dejarle 12, luego 8, luego 4… ¿Ves por qué funciona?.

Nuestro amigo Lemnismath ha inventado un "ordenador de canicas" que, si no pones atención, te ganará. Juega contra él en el Museo. Aquí tienes un video de cómo funciona.

Te proponemos otra variante. El juego es el mismo pero el que se lleva las últimas fichas, ¡pierde!. ¿Ves ahora alguna estrategia ganadora?. ¿Para el primer jugador o para el segundo?

Mosaicos aperiódicos.

Intenta formar un mosaico, es decir recubrir la superficie de la mesa con las piezas, sin superponerlas ni dejar huecos entre ellas.

En los mosaicos periódicos siempre hay un grupo de piezas que, sin más que trasladarlas, acaban formando el mosaico entero. En los mosaicos aperiódicos no existe ningun grupo de baldosas que se repita para generar el conjunto.

Te proponemos dos ejemplos:

El primero utiliza solamente dos baldosas: Con ellas es posible conseguir tanto mosaicos aperiódicos (mosaico de Penrose) como periódicos.

El segundo utiliza la baldosa Ein-stein (en alemán, una piedra) descubierta en 2023. Con esta pieza (usando su anverso y su reverso) tan sólo es posible conseguir mosaicos aperiódicos.

Más recientemente, se ha descubierto Spectre que ha resuelto el problema largamente buscado de encontrar un mosaico aperiódico realizado con una sola pieza.

Nudos y enlaces.

Este es un juego por parejas. Pon los extremos de las cuerdas alrededor de tus muñecas. Que tu acompañante haga lo mismo, pero antes, que se entrelace contigo.

El reto consiste en separaros sin sacar las cuerdas de la muñeca.

Una de las ramas de las Matemáticas estudia aquellas propiedades de los objetos que NO varían al deformarlos, estirarlos o contraerlos. Su nombre es Topología.

Quizá estéis intentando cosas que no acaban de funcionar… La maqueta que tenéis sobre la mesa pretende ayudaros a entender qué esta pasando.

Tal y como estáis entrelazados parece que sois como dos anillos enlazados. Y dos anillos NO se pueden separar. Pero la maqueta pretende dar una pista para encontrar el agujero que se necesita para la separación. ¡Quizá el monitor de sala os pueda ayudar!

Rascacielos.

La cuadrícula representa una manzana de una ciudad, formada por edificios de diferentes alturas. Los números en el exterior de la cuadrícula indican cuántos edificios son visibles en esa fila desde esa dirección. Claro, un edificio alto ocultará cualquier edificio más pequeño detrás de él.

El juego consiste en colocar todos los edificios en la plantilla cumpliendo todas las pistas que dan los números y de forma que en CADA fila o columna NO se pueden repetir alturas.

El juego tiene similitudes con los sudokus. Como en éstos, cada situación puede resolverse usando razonamiento lógico y ordenado.

En este juego es muy útil el razonamiento por reducción al absurdo. Te ponemos un ejemplo: Mmm, a ver…si pongo aquí este edificio entonces en este otro sitio tendría que poner este otro edificio y ¡vaya! resulta que acabo deduciendo que eso no puede ser porque incumple alguna regla. Por tanto, el edificio que he puesto al principio NO puede colocarse aquí.

El camino hasta llegar a la contradicción puede ser más o menos largo. Es una manera de razonar muy utilizada en Matemáticas y era una de los métodos de demostración favoritos de Euclides.

Péndulo de longitud variable.

Cuelga la cuerda del tubo horizontal y estírala del extremo libre en horizontal hasta que el peso llegue al tubo.

Cuando sueltes la cuerda...¿qué piensas que va a pasar?. ¿Se caerán el peso y la cuerda al suelo?

Se llama péndulo porque, si sujetaras la cuerda con un dedo sobre el tubo y soltaras, oscilaría como un péndulo. Sin embargo, al tener el peso en el otro lado, éste hace que la longitud del péndulo sea cada vez más corta.

El botafumeiro, el kiiking y la forma en la que te columpias para darte impulso son ejemplos de péndulo de longitud variable.

El péndulo de longitud variable es un sistema caótico. Según los pesos que se pongan en los extremos, el comportamiento puede ser muy distinto, convirtiéndolo en impredecible (o caótico).

Lo que allí pasó, en pequeño,… lo tienes delante de ti.

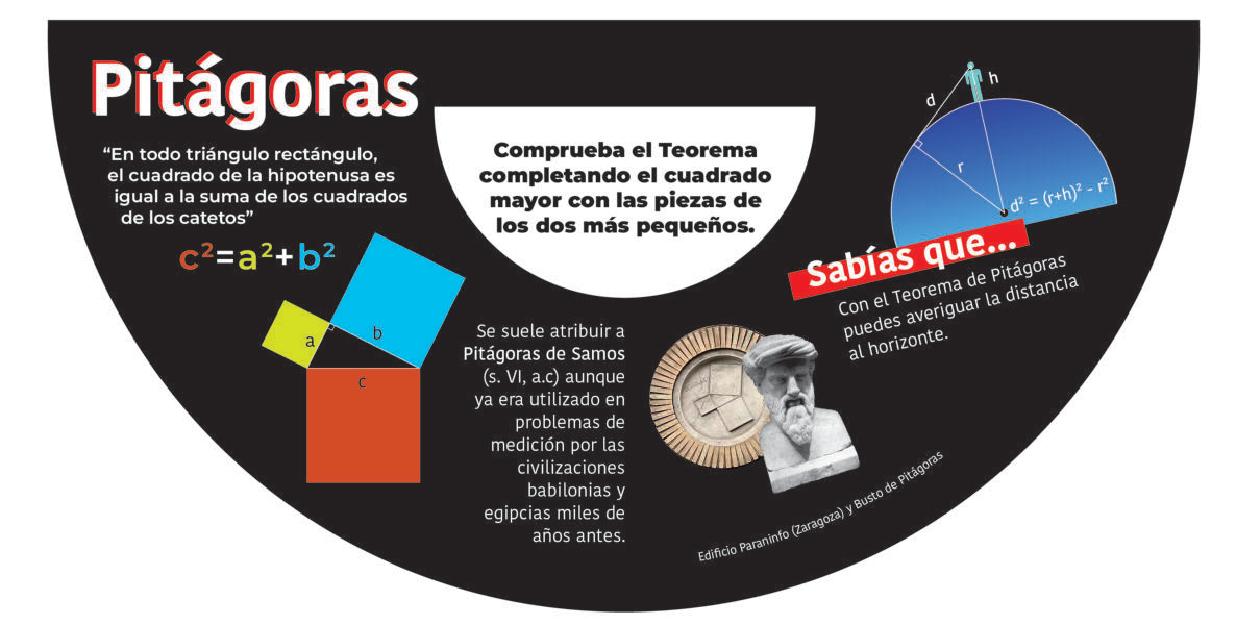
El teorema de Pitágoras.

El Teorema de Pitágoras es una conocida relación entre las longitudes de los lados de cualquier triángulo rectángulo. La actividad consiste en comprobar dicho Teorema mediante un puzzle. Se trata de rellenar el cuadrado mayor con las piezas de los cuadrados pequeños.

De esta manera comprobarás como la suma de los cuadrados de los lados menores, los catetos, es igual al cuadrado del lado mayor, la hipotenusa. ¡Ah!, y ahora ya sabes por qué el cuadrado de un número se llama así, cuadrado.

Con el Teorema de Pitágoras se puede saber a qué distancia se alcanza a ver desde, por ejemplo, la cima del Moncayo. O cómo hay que hacer de alto un faro en la costa para que su luz se vea a 20 km de distancia y así los barcos eviten unos arrecifes.

También lo puedes practicar tu mismo: Imagina que estás en la playa, puedes calcular mirando al mar a qué distancia alcanzas a ver estando sentado, o de pie... o en la habitación del hotel.

Repi-teselas (Rep-tiles).

El trapecio de la imagen y que verás sobre la mesa, puede construirse a partir de cuatro trapecios iguales pero de menor tamaño. Con las otras figuras de esta actividad te proponemos eso mismo, construir otra que tiene idéntica forma que la de sus piezas pero claro, de mayor tamaño.

En 1962 Solomon Golomb realizó el primer estudio de estas figuras auto-replicantes que bautizó como rep-tiles, una sugerente abreviatura de replicating tiles. En castellano, repi-tesela.

Durante años se creyó que la pieza de cinco lados que ves en la mesa era la única repitesela posible con cinco lados. Sin embargo hace no mucho, en 2012, se descubrieron más ejemplos. Aunque... ¡no se sabe si estan todos!

La máquina de Galton.

Deja caer las bolitas volteando la máquina de Galton. Si repitieras el experimento varias veces y pudieras concentrarte siguiendo la trayectoria de una bolita en concreto, te sería casi imposible predecir donde iría a caer. Sin embargo, las bolitas en su conjunto siempre acaban distribuidas según un mismo patrón.

Esta es una de las claves y utilidades de la Teoría de la Probabilidad. Aunque el comportamiento de individuos puede no ser predecible con exactitud, sí puede serlo el de una población completa. Y de esta forma podemos estimar la probabilidad de que una población se comporte de una determinada manera.

En la máquina de Galton, en cada choque con cada clavo las bolitas tienen una posibilidad del 50 por ciento de que reboten hacia la izquierda y otro 50 por ciento hacia la derecha. Es igual a si lanzaramos una moneda varias veces y contásemos en número de caras (o cruces). Al final de este proceso el patrón formado es, aproximadamente, el de una campana de Gauss.